数据结构与算法学习笔记03

树状结构的基础是二叉树,二叉树即度为2的树。
二叉树的链表结构
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
作业1:树的同构
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
图1:
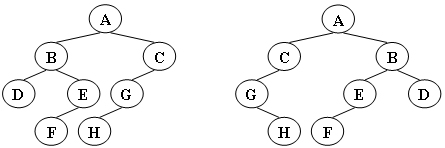
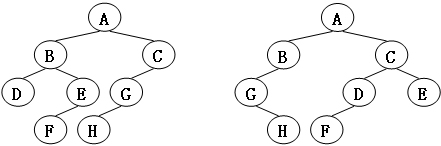
- 输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出-。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
- 输出格式:
如果两棵树是同构的,输出Yes,否则输出No。
- 输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
- 输出样例1:
Yes
- 输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
- 输出样例2:
No
- 实现:
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
//读第一个树节点
int n_a = 0;
n_a = Integer.parseInt(reader.readLine());
String[] inputs_a = new String[n_a];
List<Node> nodes_a = new ArrayList<>(n_a);
for (int i = 0; i < n_a; i++) {
inputs_a[i] = reader.readLine();
}
int n_b = 0;
n_b = Integer.parseInt(reader.readLine());
String[] inputs_b = new String[n_b];
List<Node> nodes_b = new ArrayList<>(n_b);
for (int i = 0; i < n_b; i++) {
inputs_b[i] = reader.readLine();
}
if (n_a != n_b) {
System.out.println("No");
return;
}
addNodes(inputs_a, nodes_a);
addNodes(inputs_b, nodes_b);
if(inputs_a.length==1&&!Objects.equals(nodes_a.get(0).data,nodes_b.get(0).data)){
System.out.println("No");
return;
}
for (Node node_a : nodes_a) {
for (Node node_b : nodes_b) {
if (Objects.equals(node_a.data, node_b.data)) {
if (!((Objects.equals(node_a.left, node_b.left) && Objects.equals(node_a.right, node_b.right))
|| (Objects.equals(node_a.left, node_b.right) && Objects.equals(node_a.right, node_b.left)))) {
System.out.println("No");
return;
}
}
}
}
System.out.println("Yes");
}
private static void addNodes(String[] inputs, List<Node> nodes) {
for (String input : inputs) {
Node n = new Node();
String[] lineArg = input.split(" ");
n.data = lineArg[0];
if (!Objects.equals("-", lineArg[1])) {
int left_num = Integer.parseInt(lineArg[1]);
n.left = inputs[left_num].split(" ")[0];
}
if (!Objects.equals("-", lineArg[2])) {
int right_num = Integer.parseInt(lineArg[2]);
n.right = inputs[right_num].split(" ")[0];
}
nodes.add(n);
}
}
static class Node {
String data;
String left;
String right;
}
}
- 总结:
- 利用二叉树的数据结构可以解决这个问题。
- 这里我采用了投机取巧的办法,并没有建立树状结构,而是把每个节点进行比较,唯一需要处理的特例就是同唯一父节点值不同的情况。
作业2:List Leaves(25 分)
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
- Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.
- Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
- Sample Input:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
Sample Output:
4 1 5
- 实现:
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int sum;
sum = Integer.parseInt(reader.readLine());
String[] inputs = new String[sum];
for (int i = 0; i < sum; i++) {
inputs[i] = reader.readLine();
}
int root_num = findRoot(inputs);
StringBuilder sb = new StringBuilder();
Queue<Node> nodes = new LinkedList<>();
Node root = getNode(root_num,inputs[root_num]);
nodes.add(root);
checkTree(nodes, sb, inputs);
if (sb.length() > 0) {
sb.deleteCharAt(sb.length() - 1);
}
System.out.println(sb.toString());
}
private static Node getNode(int root_num, String input) {
Node node = new Node();
node.data = root_num;
String[] lineArg = input.split(" ");
if (!Objects.equals("-", lineArg[0])) {
node.left = Integer.parseInt(lineArg[0]);
}
if (!Objects.equals("-", lineArg[1])) {
node.right = Integer.parseInt(lineArg[1]);
}
return node;
}
private static void checkTree(Queue<Node> nodes, StringBuilder sb, String[] inputs) {
while (!nodes.isEmpty()) {
Node node = nodes.poll();
if (node.left<0 && node.right<0) {
sb.append(node.data);
sb.append(' ');
}
if (node.left>=0) {
Node n_l = getNode(node.left,inputs[node.left]);
nodes.add(n_l);
}
if (node.right>=0) {
Node n_r = getNode(node.right,inputs[node.right]);
nodes.add(n_r);
}
}
}
private static int findRoot(String[] inputs) {
int[] link = new int[inputs.length];
for (String input : inputs) {
String[] lineArg = input.split(" ");
if (!Objects.equals("-", lineArg[0])) {
int left_num = Integer.parseInt(lineArg[0]);
link[left_num] = 1;
}
if (!Objects.equals("-", lineArg[1])) {
int right_num = Integer.parseInt(lineArg[1]);
link[right_num] = 1;
}
}
int i;
for (i = 0; i < link.length; i++) {
if (link[i] == 0) {
break;
}
}
return i;
}
static class Node{
int data =-1;
int left = -1;
int right = -1;
}
}
- 总结:
- 树的遍历最基本的方法是采用递归;
- 使用堆栈可以免递归遍历树,每个对象有3次访问机会,调整访问时机可以分别实现前序、中序及后序遍历;
- 采用队列可以层级遍历树,此题采用层级遍历。
作业3:Tree Traversals Again(25 分)
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
- Figure 1
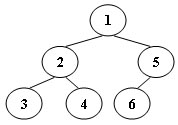
- Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
- Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
- Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
- Sample Output:
3 4 2 6 5 1
- 实现:
package cn.wycode;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Objects;
import java.util.Stack;
public class Main {
public static void main(String args[]) {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
//读第一行
String[] line1Array = getStringArray(reader);
String firstAddress = line1Array[0];
int count = Integer.parseInt(line1Array[1]);
int k = Integer.parseInt(line1Array[2]);
//读取所有节点
ArrayList<Node> nodes = new ArrayList<>(count);
for (int i = 0; i < count; i++) {
String[] lineArray = getStringArray(reader);
Node node = new Node();
node.address = lineArray[0];
node.data = Integer.parseInt(lineArray[1]);
node.nextAddress = lineArray[2];
nodes.add(node);
}
//按链表顺序加入队列
LinkedList<Node> queue = new LinkedList<>();
String address = firstAddress;
while (!address.equals("-1")) {
for (int i = 0; i < nodes.size(); i++) { //循环匹配地址
Node n = nodes.get(i);
if (Objects.equals(address, n.address)) { //找到则加入队列
queue.add(n);
address = n.nextAddress; //查找地址赋值为当前节点的下一个地址
nodes.remove(n); //处理完的移出节点数组,减少循环量
break;
}
}
}
Stack<Node> stack = new Stack<>();
boolean isCanConvert = queue.size() >= k; //是否够反转
while (!queue.isEmpty()) { //循环出队列
Node n = queue.remove();
if (isCanConvert) { //够反转则压入堆栈
stack.push(n);
if (stack.size() == k) { //压够反转数量就全部输出
isCanConvert = queue.size() >= k; //再次检查是否够反转
while (!stack.isEmpty()) {
//重新赋值next
Node nStack = stack.pop();
if (stack.isEmpty()) { //如果栈里没了,地址就等于队列的下一个
if (queue.isEmpty()) { //队列也没了,地址等于-1
nStack.nextAddress = "-1";
} else {
//如果剩下的还能反转
if (isCanConvert) {
nStack.nextAddress = queue.get(k - 1).address;
} else {
nStack.nextAddress = queue.peek().address;
}
}
} else {
nStack.nextAddress = stack.peek().address;
}
print(nStack);
}
}
} else { //不够反转 直接输出节点
print(n);
}
}
}
private static void print(Node n) {
System.out.println(n.address + " " + n.data + " " + n.nextAddress);
}
private static String[] getStringArray(BufferedReader reader) {
String line1 = null;
try {
line1 = reader.readLine();
} catch (Exception ignore) {
}
return line1.split(" ");
}
static class Node {
String address;
int data;
String nextAddress;
}
}
- 总结:
- 利用队列和栈解决顺序问题
作业2:Pop Sequence(25 分)
Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.
Input Specification:
Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.
Output Specification:
For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.
Sample Input:
5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2
Sample Output:
YES
NO
NO
YES
NO
- 实现
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int sum;
sum = Integer.parseInt(reader.readLine());
String[] inputs = new String[sum*2];
for (int i = 0; i < inputs.length; i++) {
inputs[i] = reader.readLine();
}
StringBuilder sb = new StringBuilder();
//Build Tree
Node root = buildTree(inputs);
//后序遍历打印
traversalsTree(root,sb);
if (sb.length() > 0) {
sb.deleteCharAt(sb.length() - 1);
}
System.out.println(sb.toString());
}
private static Node buildTree(String[] inputs) {
Node root =null;
Stack<Node> nodes = new Stack<>();
final String PUSH = "Push";
final String POP = "Pop";
Node lastPush = null;
Node lastPop = null;
String lastOperation = null;
int level = 0;
for (String input : inputs) {
String[] lineArg = input.split(" ");
if (Objects.equals(lineArg[0], PUSH)) {
Node node = new Node();
node.data = Integer.parseInt(lineArg[1]);
node.level = level;
nodes.push(node);
if (lastOperation == null) {
root = node;
} else if (Objects.equals(lastOperation, PUSH)) {
lastPush.left = node;
} else if (Objects.equals(lastOperation, POP)) {
lastPop.right = node;
}
lastPush = node;
lastOperation = PUSH;
level++;
} else {
lastPop = nodes.pop();
lastOperation = POP;
level--;
}
}
return root;
}
private static void traversalsTree(Node root, StringBuilder sb) {
if(root!=null) {
traversalsTree(root.left, sb);
traversalsTree(root.right, sb);
sb.append(root.data);
sb.append(' ');
}
}
static class Node {
int data = -1;
Node left;
Node right;
int level = 0;
@Override
public String toString() {
return "Node{" +
"data=" + data +
", left=" + (left==null?"null":left.data) +
", right=" + (right==null?"null":right.data)+
", level=" + level +
'}';
}
}
}
- 总结:
- 通过先构建出原始树再后序遍历的方法解决了问题。
- 优化方向:将后序遍历的递归方式改为非递归方式。
- 此题应该可以在构建树时直接输出正确答案。
- 非递归算法核心:
首先要搞清楚先序、中序、后序的非递归算法共同之处:用栈来保存先前走过的路径,以便可以在访问完子树后,可以利用栈中的信息,回退到当前节点的双亲节点,进行下一步操作。 后序遍历的非递归算法是三种顺序中最复杂的,原因在于,后序遍历是先访问左、右子树,再访问根节点,而在非递归算法中,利用栈回退到时,并不知道是从左子树回退到根节点,还是从右子树回退到根节点,如果从左子树回退到根节点,此时就应该去访问右子树,而如果从右子树回退到根节点,此时就应该访问根节点。所以相比前序和后序,必须得在压栈时添加信息,以便在退栈时可以知道是从左子树返回,还是从右子树返回进而决定下一步的操作。
 青衿AI
青衿AI